Welcome to what I hope to be the first of several tutorials on Algorithms for Computer Algebra. I've seen several people express an interest in the subject for the purposes of learning how to write a CAS, so I thought I'd share one of the most commonly desired algorithms: Symbolic Differentiation. As we all learn in Calculus, Differentiation is the operation of finding the function describing the slope of a curve at any point along that curve. There are many different ways of doing this, all of which are equivalent. Some involve heuristic rules, such as those taught in standard Calculus, while others might involve insane projections onto new spaces, simplifying the differentiation operation dramatically. However, Diffferentiation is almost always done in what is called the Euclidean plane (the XY plane we all
hate know and love), so that's where this tutorial will focus.
Symbolic math in Computer Programming often relies quite heavily on String manipulations. Differentiation is no different. Keep in mind while reading this that familiar operations such as Addition may not be as simple as using the available CPU addition instructions.
Differentiation is an excellent example of a difficult problem to implement in software. When one first tackles it, the immediate problem one encounters is how to represent functions so that the operation can be written and tested. This is precisely the wrong way to go about solving it. Let us first go back to class and see how we learned how to differentiate on paper.
If you took the same classes I did, then you learned to differentiate through the use of limits. The derivation probably went something like this:
Let the derivative be the slope of the curve at a point (X,Y). We will denote the change in x at (X,Y) as Δx and the change in y at (X,Y) as Δy. If the curve is linear, then the slope at (X,Y) is
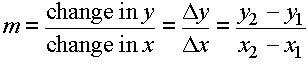
Next, let us observe that many functions are approximately linear in the neighborhood near a point. If we substitute h for Δx and g for Δy, then for a curve f(x)=y, the slope at a point is approximately
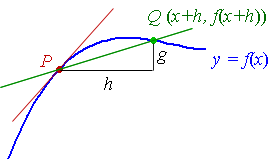
As we make h and g smaller and smaller, the approximation becomes closer and closer to the true tangent. To do this, we take the limit as h goes to 0 (meaning g also goes to 0).
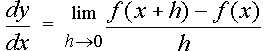
Thus, we have arrived at the geometric definition of a derivative. However, it's completely useless for computers. Finding limits is
hard; harder than finding a derivative in fact (particularly for multivariate functions, where limits become extremely difficult to determine). We need a new method to try.
Another method is more algorithmic and algebraic in nature. It's typically taught in the middle of the first semester of Calculus and involves the use of rules. Rules such as the Product rule (d/dx f(x)g(x) = f(x)g'(x)+f'(x)g(x) ) as used to break functions down into simpler components. These methods were the basis of the original Symbolic Differentiation programs and remain important today. For our algorithm, we'll be using several rules: the Product Rule, the Chain Rule, the Power Rule, the Logarithmic Differentiation method, the Constant Rule, and the Addition Rule. These will be used to break the function down into simpler parts.
Rules table:
d/dx h(x) = ?
Case 1: h(x) = C*f(x)
d/dx h(x) = C * d/dx f(x)
Case 2: h(x) = x
nd/dx h(x) = nx
n-1 except when n=0Case 3: h(x) = f(x)+g(x)
d/dx h(x) = d/dx f(x) + d/dx g(x)
Case 4: h(x) = f(x)g(x)
d/dx h(x) = f(x)g'(x)+f'(x)g(x)
Case 5: h(x) = f(x)/g(x)
d/dx h(x) = h(x)( f'(x)/f(x) - g'(x)/g(x) )
Case 6: h(x) = f(x)
g(x)d/dx h(x) = ( f(x)
g(x)-1 )g(x)f'(x)+f(x)
g(x)Log
e(f(x))g'(x)
Case 7: h(x) = Log
e(f(x))
d/dx h(x) = f'(x)/f(x)
Case 8: h(x) = C
d/dx h(x) = 0
This covers all elementary functions, so any function that can be input can be differentiated using these rules.
Let's try an example:
h(x) = xLog
e(x)
h(x) = f(x)g(x) where f(x) = x and g(x) = Log
e(x).
d/dx h(x) = f(x)g'(x)+f'(x)g(x)
d/dx h(x) = x(1/x)+1*(Log
e(x))
d/dx h(x) = 1+Log
e(x)
