This section allows you to view all posts made by this member. Note that you can only see posts made in areas you currently have access to.
Messages - Chockosta
1
« on: November 25, 2013, 03:22:36 pm »
I used NoShell with my 83+BE, that's probably what caused the crash.
I'll try with MirageOS then (DCS is too heavy for my calc)
2
« on: November 25, 2013, 03:18:20 pm »
Congrats on the feature! I played it a little today, and I got to stage 4, but when I quitted, the program crashed and I lost my progress  Apart from this crash, it is very polished and fun. I'll probably try to beat it in one go, to avoid crashes!
3
« on: November 22, 2013, 02:00:59 pm »
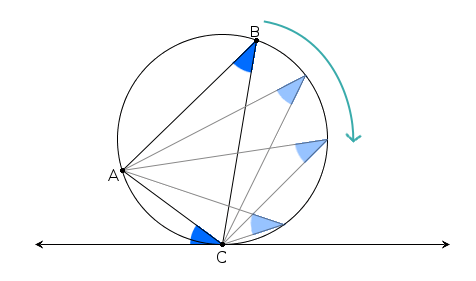
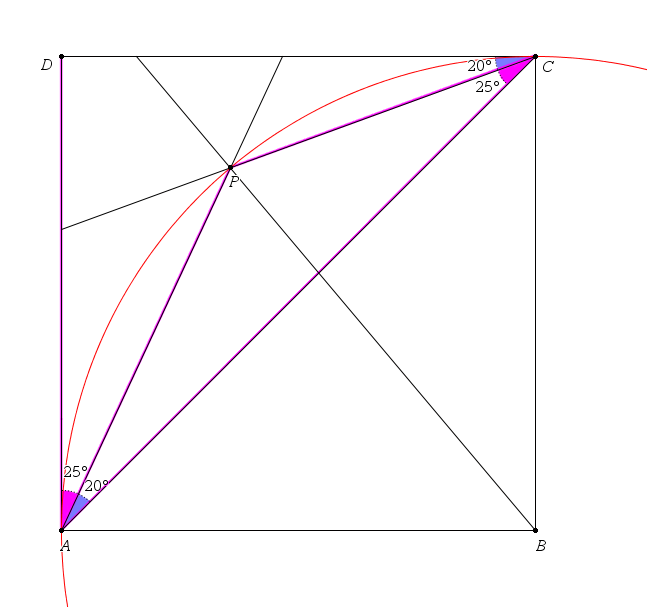
Thanks for those drawings, but they only show the easy part of the proof. The interesting part is that B is the center of the drawn circle, which is true if and only if PAC=PCD. Here are some drawings : The inscribed angle theorem says that the blue angle remains the same when you move B. (This is a well-known and useful result) The corollary of this theorem says that it is the same as the angle with the tangent in C. (To understand this, keep in mind that the blue angle doesn't change when B is getting close to C) In this drawing you can notice that the purple angles are acting the same way as mentionned before. Therefore, you can say that AD is tangent to the circle in A. Moreover, you can do the same with the blue angles. So CD is tangent to the circle in C. Since ABCD is a square, CB is perpendicular to CD in C. But CD is tangent to the circle in C. Therefore CB is a radius of the circle. You can do the same and find that AB is also a radius. The two radii meet in B, so B is the center of the circle. The conclusion is now quite obvious, see SpiroH's drawings I personnally did it with the inscribed angle theorem : You can apply this to PAC and PBC and find out that PBC=2*PAC, so PBC= 40°
4
« on: November 21, 2013, 04:26:42 pm »
Hey, I was passing by and I just saw this topic.
Runner's solution works, but using analysis for such a problem is sad.
I found this nice solution in 5 minutes :
- Clearly PCA=PAD=20°
- Let O be the circle that passes through P, C, A
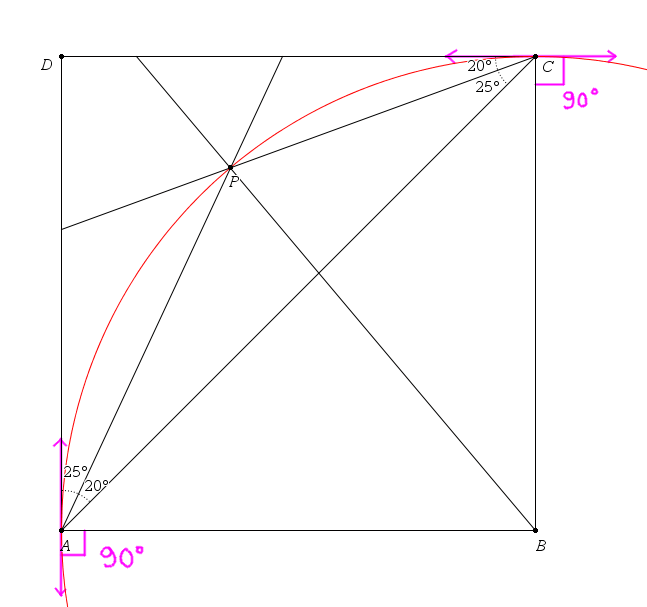
- Since C and A are on O and PCA=PAD, DA is tangent to O in A (corollary of inscribed angles theorem)
- DA and AB are perpendicular so AB passes through the center of O
- Since C and A are on O and PCD=PAC, DC is tangent to O in C
- DC and CB are perpendicular so CB passes through the center of O
- Hence the center of O is the intersection of AB and CB, B
- Since B is the center of O and P, A belong to O, PBA=2*PCA=40°
I hope you can understand despite my poor English
5
« on: June 11, 2013, 12:17:32 pm »
Wow, this looks pretty good ! My question to chokosta is : can i use the lvl and the design of gravity guys nspire for my game if i quote you in my credit ?
Of course. You don't have to quote me, since my programs are totally free. Anybody could re-use my code and sell it. IIRC chockosta's version was inspired by mine lol
No, I discovered your gravity guy a few days after starting mine. My game was more inspired by the android version. (The gravity is linear in my game and the android app, but not in your version) I don't think that you could switch gravity in mid-air in any version of Gravity Guy. That's what made the game hard to beat.
Indeed, that would make it trivial.
6
« on: June 11, 2013, 11:16:35 am »
Well, I guess I beat it. I'm not sure, because there's no ending scene, just no more enemies.
It wasn't really hard, though. I didn't use any bomb. Remember that we're speaking about a danmaku programmed in Axe on a 83+ non-SE, intended to run correctly and be playable at 6 MHz, and not even finished 
Yeah, sorry, I forgot the most important : Great job ! This is one of my favorite z80 games so far. The engine is really fun to play with, and the levels are well designed. (except for the level 3 boss pop-up  )
7
« on: June 11, 2013, 10:49:21 am »
Hey there !
I have stopped programming for a while, and currently I'm into danmaku (Touhou addiction, to be more specific)
I was passing by, and I decided to give your game a try.
Well, I guess I beat it. I'm not sure, because there's no ending scene, just no more enemies.
It wasn't really hard, though. I didn't use any bomb.
The only hard part is when the level 3 boss spawns right on your hitbox.
I'm looking forward to harder levels !
I recommend using more aimed bullets, and streaming-based levels.
8
« on: May 11, 2013, 05:32:07 pm »
Yeah, and the three playable character are Reimu, Marisa and Sakuya.
It seems very promising, and I hope that it will be better than TD and UFO (which are still very good games)
I'm looking forward for the demo !
9
« on: April 13, 2013, 12:33:38 pm »
There's a new demo, with netplay and a new stage ! (But still only 3 characters) You can download it on Tasogare frontier official website : http://www.tasofro.net/touhou135/index.html#130412So, does anybody want to play ?
10
« on: March 24, 2013, 07:52:29 am »
Last year, I used to play this quite a lot, and I think I have the high score : 1,571,515
Yeah, I love shoot em ups...
11
« on: February 20, 2013, 10:10:23 am »
I never saw this bug, this is very strange.
Which OS are you using ?
And what do you mean by "the document is sometimes just blank" ? Is the document totally empty or is it the Lua script app which is blank ?
12
« on: January 21, 2013, 01:04:10 pm »
If he does, I hope he told it Chockosta la vista
That is one epic line 
Yeah, awesome  But, as always, I'm sorry for not being able to bring you updates. For now, I don't spend my free time coding, but playing... As always, when someone bumps this thread, I feel very motivated and go back to my code, but that motivation quickly disappears and I feel very bad for making you wait like that. And I don't even have an excuse...
13
« on: January 21, 2013, 12:56:45 pm »
Sure ! My programs aren't under any license.
You can use them, and even get all the credit for it. (But I'd appreciate if you mention my name)
The source code is attached to this post.
14
« on: January 08, 2013, 12:17:36 pm »
I made a simple clipped triangle routine. I can share it, if you're interested.
Yeah i*3 is a small but good optimization.
15
« on: January 06, 2013, 10:07:51 am »
No, not necessarily.
Actually, they can be as far as you want, if they are in the field of view cone. (The only restriction is that the x-coordinate can't be negative)
That's why if you want to keep a good speed, you should check if vertices are not too far before drawing them.
Here is the function that I use in nCraft :
-vertices* is an 1D array with 3D coordinates of used vertices. (example : {5,0,0, 5,1,0, 5,1,1 5,0,1})
-pos* is an 1D array when I will store the 2D coordinates of projections (example : {50,50 100,50 50,100 100,100})
-size is the number of vertices
void computeVertices(float *vertices,int *pos,int size)
{
int i=0;
float temp=0.0;
for(i=0;i<size;i++)
{
if(vertices[i*3+1]>0)
{
temp=OFFSET*vertices[i*3]/vertices[i*3+1]*50.0+160.0; //offset is an arbitrary value. I use 10.
pos[i*2]=(int)temp; //screen coordinates have to be integers
temp=-OFFSET*vertices[i*3+2]/vertices[i*3+1]*50.0+120.0;
pos[i*2+1]=(int)temp;
}
else
{
//if vertices are behind the camera, I store arbitrary values to remember not to draw them
pos[i*2]=-10000;
pos[i*2+1]=-10000;
}
}
}
|