What about that  :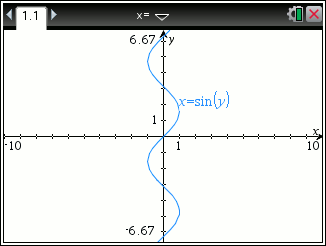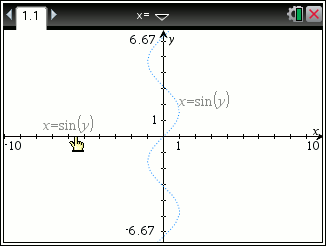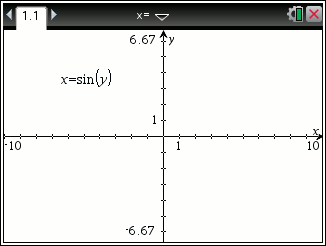





This is coming with 3.2

Quote from: Lionel Debroux on March 04, 2012, 02:30:29 pm

Quote

However, I am not sure if that would make them change their mind.

Rather, I am sure that it would not make them change their mind

Agreed - gaming is probably on the teacher's "no-no" list, so it is probably on TI's too.

From what I've seen during the T3 conference, it depends what kind of gaming
Sure, nDoom is probably not the best option

But things like TI-basket or any other game that could involve math and/or physics inside, can interest TI and the teachers, really.

That's also why they did the physics engine : having realistic simulations of physical stuff hapenning, in order to better studies real-life cases

I just edited the news since Critor was referring to me directly and what I said and Melendy Lovett, so I thought I had to edit it.

Here's what I added (it was about Ndless blocking on 3.2, when I met Melendy Lovett) :

(These are examples that I myself refer to, I don't think she was the one to bring these examples in.
What she insisted on, and I think it's fair to write about this here, in order to have some objectivity, is that TI is liked "ruled" by its clients, and its main clients are teachers and schools. Meaning that they have to make what teachers want, and they listen to teachers and what they say. Since TI and the teachers are really close, TI can't really allow multiple opposite "development directions", and rather than do as what the community would like, they have to align with what the teachers want, most often. The thing is that there is a real trust relationship between TI and the teachers, and TI thus can't lose this trust by providing tools/devices that can (in the bad case, but since it's a possibility that cannot be marginal, it has to be said) not be trusted because some people can crack it and do things they normally wouldn't be able to do. As teachers want to feel safe about TI products, TI has to provide such products, that's why they try to block Ndless at each update : "protect the teachers" to avoid losing the trust they have established.)


So, maybe this explanation(s) from TI are new for some of you (it was for me at the time), and there are valid arguments on both the community side and the teacher side, but since on this forum, it's the community who is represented, I don't think I'm going to have much success in talking a lot about TI's "closed" Nspire (even though they made a great step ahead with Lua !).

Anyway, as people said, it's always like a game between TI and Ndless, and if it's actually blocked in 3.2, it's also going to get cracked at some point, but it's going to take a while, and that's sad for people who just want to have full access to a device they bought...

I personally think that, even if I'm a TI-Planet co-admin, a lot more people would go update to 3.2 even if they know they'll lose ndless, because TI made honestly some great efforts in this 3.2 update.
The Lua inside is really great (Native Physics Engine binding is ... wow !), there are a numbers of bug fixes and a number of new features, and this can be a game changer for people who were on ndless'd OSes before but didn't really used ndless programs that often. (And I'm an example of this kind of people. I obviously do enjoy nDoom, GBC4nspire, mViewer, etc. and it certainly won't be replaced by whatever TI will do, this is sure), but as I'm a Lua fan, I'll have to update to stay at the latest things available...
(Oh well, I guess it's nice that I have multiple CX to have multiple OSes with ndlessed ones and official ones...



Anyway... Thanks for reading that long post, maybe some of you will find it interesting.

That looks really nice !

Trying on nspire_emu

Well, now, there are several ways to do it  :
- Using a memory dumper and extract what you want from nspire_emu
- Using any Clipboard dumper while having copied a Lua widget from within the computer software. (levak made a little software for that, on Windows)
- Using the official Lua SDK (which will be released "soon" (?) ), from which you'll be able to directly edit the lua code from within the .tns file, obviously.

These
(see attached : it's a math homework about calculating limits of the functions written)


(maybe some of them are doable, but probably not all)
(since you can't always take the derivative (easily))

I just read that on Wikipedia, and it's pretty good
(warning : quite high level math...)

Abstract algebra
Any number system that forms a commutative ring — for instance, the integers, the real numbers, and the complex numbers — can be extended to a wheel in which division by zero is always possible; however, in such a case, "division" has a slightly different meaning.
The concepts applied to standard arithmetic are similar to those in more general algebraic structures, such as rings and fields. In a field, every nonzero element is invertible under multiplication; as above, division poses problems only when attempting to divide by zero. This is likewise true in a skew field (which for this reason is called a division ring). However, in other rings, division by nonzero elements may also pose problems. For example, the ring Z/6Z of integers mod 6. The meaning of the expression  should be the solution x of the equation 2x = 2. But in the ring Z/6Z, 2 is not invertible under multiplication. This equation has two distinct solutions, x = 1 and x = 4, so the expression  is undefined.
In field theory, the expression  is only shorthand for the formal expression ab−1, where b−1 is the multiplicative inverse of b. Since the field axioms only guarantee the existence of such inverses for nonzero elements, this expression has no meaning when b is zero. Modern texts include the axiom 0 ≠ 1 to avoid having to consider the trivial ring or a "field with one element", where the multiplicative identity coincides with the additive identity.

( http://en.wikipedia.org/wiki/Division_by_zero#Linear_algebra )


Also :

To show how division by zero does not work with the rules or mathematics we can use the associative law of multiplication and the fact that 0x2=0


We can use the rules of arithmetic to show 0x2=0 as follows:
given 2 is defined as 1+1=2 then
M1 tells us that 0x2=2x0
D tells us that (1+1) x0 = 1x0 + 1x0
But M3 tells us that 1x0=0
so this equals 0+0
finally A3 implies 0+0=0



Now having proved 0x2=0 we can use this with M2 to give
1 = inf x 0 = inf x (0x2) = (inf x 0) x 2 = 1 x 2 = 2

Since 1 does not equal 2 then an inconsistency with the most basic rules of numbers and as such division by zero does not work with these rules.



M1: The commutative law of multiplication states:
ab=ba
for any two numbers a and b

M2: The associative law of multiplication states:
a(bc) = (ab)c
for any 3 numbers a, b and c

M3: The multiplicative identity:
1a = a
for any number a

The distributive law states:
(a+b)c = ac + bc
for any three numbers a, b and c

A3: The additive identity:
0+a=a
for any number a