This section allows you to view all posts made by this member. Note that you can only see posts made in areas you currently have access to.
Messages - christop
31
« on: August 07, 2011, 01:44:37 am »
Um, fractions aren't defined for INTEGER data types, which are all the Windows calculator deals with in programmer mode.
That was basically the point of my gripe: that it supports only integers in Programmer mode. It would be nice if it supported fractions in hexadecimal, octal, and binary. (Hexadecimal/octal/binary are not integer types; they are bases). For example, if I want to see what 2.375 is in binary, I use the standard Gnome calculator (gcalctool) and switch to binary. 2.375 decimal is 10.011 in binary, 2.6 in hexadecimal, or 2.3 in octal. It's really handy for calculating fixed-point values, for example (which is a common task in some areas of PROGRAMMING), but the Windows calculator can't do this basic task.
32
« on: August 06, 2011, 10:52:57 pm »
As I've been posting here at Cemetech, I have a working routine now. It's not necessarily the most optimized but it's pretty quick (it runs in 1824 cycles). Here's a screenshot showing a little test program multiplying a few inputs: 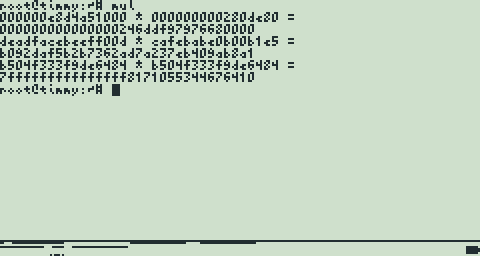 If you're so inclined, you can double-check the results yourself.  On a somewhat but not too related note, the Windows calculator sucks. It can't do fractions in "Programmer" mode, and that's the only mode that supports different bases (eg, hexadecimal), which means it can't calculate hexadecimal fractions like 1.6A09E667F. Microsoft must think that programmers don't (or can't) use fractions. I'm a programmer, and I do in fact use fractions at work! It also uses weird keyboard shortcuts like Y for exponentiation or F9 for negate. The only sensible keyboard shortcuts are the keys 0 through 9 and +-/*. Lame. Fortunately, I use Linux at home, so I don't have these problems at home. gcalctool FTW!  </rant>
33
« on: August 06, 2011, 12:06:03 am »
Continuing from my last post, here's what I've gotten so far. I decided to start with a plain 64x64->128 multiplication routine but with a few optimization tricks.
First of all, this routine will have to execute 16 multiply instructions, since there are four 16-bit words per 64-bit value (4*4=16), as I noted in my previous post. To make the rest of this post make more sense, I've numbered all 16 of these 32-bit products:
00 11 22 33 ae af ag ah
44 55 66 77 = be bf bg bh
88 99 aa bb ce cf cg ch
cc dd ee ff de df dg dh
The first little optimization I thought to do is to push the first 4 32-bit products onto the stack (storing the 128-bit result on the stack). The first four products are 00 (88|55|22) (dd|aa|77) ff, where (...) provides a few different options in that position. I wanted to minimize the number of swaps needed to multiply these products (swaps are needed to put the appropriate 16-bit value in the lower 16 bits of the register that contains that value), so I chose the products 00 88 dd ff. This sequence requires only two swaps. (I actually calculate them in reverse order--ff dd 88 00--so that 00 ends up at the top of the stack (lowest address) because it's the most significant word, and we're storing values in big endian). From here I was just thinking about calculating the remaining 12 products and add them to the current 128-bit result, with carry, using inline loops (or unrolled loops). Either that, or push each of them onto the stack as individual partial products and add them all with carry.
The second optimization I thought of is to combine or "pack" the products together into partial products like the first one. This gave me the following seven partial products:
0088ddff
.44ccee.
.1199bb.
..55aa..
..2277..
...66...
...33...Then I would add up only seven partial products rather than 13 (or worse, 16). Note that the ordering of the products within each partial product is somewhat arbitrary. I could have used the partial products ..5577.. and ..22aa.. instead of ..55aa.. and ..22aa.., for example. They add up the same either way.
The last optimization tick comes from a recent realization of mine: the maximum product of two unsigned 16-bit values is 0xFFFE0001. What this means is that staggered long (32-bit) values can be added together without carry. Here's an example:
FFFE0001
+ FFFE0001
+ FFFE0001
----------------
FFFEFFFFFFFF0001This addition can be extended to any number of staggered longs without carry.
This optimization resulted in the following layout:
first partial product:
0088ddff +
.44ccee.
second partial product:
.1199bb. +
..55aa..
third partial product:
..2277.. +
...66...
fourth partial product:
...33...
The first partial product is calculated by adding the first set of products (00 88 dd ff) and the second set of products (44 cc ee) without carries, since they are staggered from each other. The second partial product is calculated similarly and is then added to the first partial product (using addition with carries). The third and fourth partial products are also calculated and added to the result in turn. Afterwards, the 128-bit result on the stack is popped off into the registers %d0-%d3 (with a single movem.l (%sp)+,%d0-%d3 instruction) and the routine returns.
Using this staggered-add trick, I just have to add up 4 partial products with carry instead of 16 or even 13. Hopefully I can find a few other tricks like this to help speed up the routine even more.
The stack usage of this routine will be 256 bits, or 32 bytes. I might be able to reduce that by storing part of the 128-bit result in registers and part of it on the stack, which will surely complicate it more but might also make it a bit faster as well.
UPDATE: I finally implemented a working multiply routine, almost exactly as I described it here. It takes a bit more than 32 bytes of stack space, though, since it has to save a few registers. My first test was to multiply 0x000000E8D4A51000 (1e12 decimal) by 0x000000000280DE80 (42e6 decimal) to get the product 0x000000000000000246DDF97976680000 (42e18 decimal), which the routine managed to compute correctly after a few bug fixes. I'll need to test some larger values to ensure that all bits are touched with non-zero values.
Right now the routine takes 2326 cycles, which isn't too bad but not that great either. The 16 multiplies account for just over half of that (1184 cycles), so I may be able to reduce the total by a few hundred cycles with some additional optimizing.
34
« on: August 04, 2011, 01:28:47 am »
So I'm still working on the file system. There's not much to show for it yet, but I've cleaned up a lot of old code and designed a generic file system interface (so additional file systems can be added by following the same interface). I also started writing a simple RAM-based file system (tmpfs) just to get the rest of my code off the ground (I won't have to debug the block cache, the FlashROM driver, and a complex FlashROM file system all at the same time). On the user-visible side, I added a couple new user commands in the shell: bt and crash. They're pointless for users, but they are somewhat useful for me.  The crash command crashes the current shell a number of different ways (address error, division by zero, chk instruction, trap on overflow, privileged instruction, line 1010 emulator, line 1111 emulator, and invalid memory access). In each of these cases, the kernel catches and reports the exception and sends the appropriate signal to the process (such as SIGFPE for division by zero), which kills the process. On the kernel side I also completed the trap handlers for all of these cases. The kernel actually can handle 3 additional traps--bus error, illegal instruction, and instruction trace--but I just didn't add them to the crash command yet. Here's an actual crash session:  SIGILL SIGILL (signal 4 here) is raised when executing a privileged instruction. Side note about the line 1111 emulator: this is used for trapping FPU instructions (all these operands start with the bits 1111) so they can be either emulated or passed to the appropriate FPU hardware (which the TI-9x don't have). I chose to emulate FPU instructions for the benefit of user programs, so running "crash 1111" will not crash the process if my FPU emulator is enabled. The bt command prints a backtrace of the current process, meaning it shows each return address starting at the most recent (this relies on the frame pointer being used as it's intended, which isn't the case with some compiler optimization options).
35
« on: August 03, 2011, 10:28:38 am »
I'm actually writing a floating-point library!  I've already figured out the math behind 64-bit multiplication using only 16-bit multiplies: (1000a+100b+10c+1d)*(1000e+100f+10g+1h) =
1000000ae + 100000af + 10000ag + 1000ah +
100000be + 10000bf + 1000bg + 100bh +
10000ce + 1000cf + 100cg + 10ch +
1000de + 100df + 10dg + 1dh
(Each digit represents 16 bits, since I'm multiplying two 16-bit "digits" at a time.) Here's where each of the half-products falls into place in the final 128-bit product: ah
bg
cf
de
ag dh
bf ch
ce dg
af bh
be cg
ae df
00000000
Obviously, if I'm going to use only the top 64 bits (top 4 digits), I have to calculate at least ten half-products. The remaining five half-products may or may not affect the sum, so some of them can possibly not be calculated. It depends on whether their sums carry into the upper 64 bits. The trick is to do this quickly in 68k asm. FWIW, the TI-AMS floating-point format uses 16 BCD digits in 64 bits, so TI-AMS has to multiply values in 4-bit or 8-bit units. I know PedroM pre-multiplies one of the operands by the values 0 through 9 (using only addition and subtraction), but it still has to perform a lot of multiply instructions. My code uses 80-bit extended-precision IEEE754 floating-point values, so it should be faster, even with all 16 multiply instructions. Plus this will give me more than 19 decimal digits of precision vs 16 decimal digits with TI-AMS floats. On the other hand, float->decimal and decimal->float are slower than with BCD, but I expect those operations to be performed less often than pure math operations.
36
« on: August 03, 2011, 01:47:29 am »
Hi all! I am in search of a fast routine that can multiply two 64-bit unsigned integers and return a 128-bit unsigned integer. Preferably the inputs are in %d0:%d1 and %d2:%d3, and the output is in %d0:%d1:%d2:%d3, but I'll take what I can get if the order is different (perhaps the product can be in %d4:%d5:%d6:%d7). Does anyone know where I can find such a routine? Another option is a routine that can multiply two 1.63 fixed-point values and return a 2.62 fixed-point product (or, preferably, normalized to 1.63). Such a routine might be faster than shifting a 128-bit product and dropping the lower 64 bits, as there may be no need to calculate all of the low-order bits--just the ones that influence the upper 64 bits. On a somewhat related topic, I also need a 64-bit division routine (64 / 64 => 64), also normalized.  In case you're curious what I need this for, I'm writing a floating-point library which uses 64-bit significands, and I have to multiply these significands for the multiplication floating-point operation. The significand can be thought of as a normalized 1.63 fixed-point value, which means the high bit (the integer part) is always 1. As such, the product "p" of two 1.63 fixed-point values (a 2.62 fixed-point value) must be 1.0 <= p < 4.0.
37
« on: March 27, 2011, 06:02:51 pm »
I hope this helps a bit, although we can't do much about number 1, unless someone released a third-party z80 emulator for the TI-Nspire (which could take years).
The Gameboy Color (emulated by gbc4nspire) actually uses a Z80-derived processor, so if Brendan Fletcher (author of gbc4nspire) wants to and has the time to write a TI-83+/84+ emulator, we may have one within a year. If you really want one, see if he is interested in writing it. 
38
« on: March 27, 2011, 05:48:10 pm »
The calculator I/O port uses a 2.5mm stereo cable, and ASM has direct control over the "left" and "right" channels, so it's only a matter of Axe supporting it.
39
« on: March 27, 2011, 05:23:54 pm »
Here's my office, which is quite messy (just like most of your guys' caves  ): ):
http://i3.photobucket.com/albums/y64/abbrev/cave-pano.jpg
Please excuse the parallax errors. I was taking a very quick panorama.
And here's my collection of Commodore equipment in the corner:
http://i3.photobucket.com/albums/y64/abbrev/cave-corner.jpg
In the stack I have a C128 at the bottom, a C64 in the middle, and a C16 at the top. I have two 1541 floppy drives (only one shown here), one 1571 floppy drives, and a 1802 color monitor. I have other Commodore peripherals not shown here too, such as joysticks, a printer, a Koalapad, a tape drive, and paddles. And, of course, lots of floppy disks. 
I want that corner of Commodores..
THEY'RE MINE! YOU CAN'T HAVE THEM!  My family's had that C64 since I was a child. I learned BASIC on it when I was 6, so I'm never going to give it up, or let it down! I won't run around or desert it either.
40
« on: March 27, 2011, 05:19:23 pm »
I noticed the music stand, what do you play?
My wife is the musician. She can play guitar (not very well  ), flute, and oboe, and I think also the piano. I can only play CD's and MP3 players (and the piano, but very very little). 
41
« on: March 27, 2011, 05:02:26 pm »
Here's my office, which is quite messy (just like most of your guys' caves  ): http://i3.photobucket.com/albums/y64/abbrev/cave-pano.jpgPlease excuse the parallax errors. I was taking a very quick panorama. And here's my collection of Commodore equipment in the corner: http://i3.photobucket.com/albums/y64/abbrev/cave-corner.jpgIn the stack I have a C128 at the bottom, a C64 in the middle, and a C16 at the top. I have two 1541 floppy drives (only one shown here), one 1571 floppy drives, and a 1802 color monitor. I have other Commodore peripherals not shown here too, such as joysticks, a printer, a Koalapad, a tape drive, and paddles. And, of course, lots of floppy disks. 
42
« on: March 26, 2011, 04:20:00 pm »
I took SirCmpwn's challenge/dare. Here's my own tiny sprite converter for the TI-86. It's 39 bytes of code/53 bytes on calc. It might be one byte larger if you port it to the 83+ because you can't jump straight to a bcall (or can you?). EDIT: Derp, I finally saw the mistake in one of the comments. Where it says "height" in "height of graph screen in bytes", it should say "width". Oh well. 
43
« on: March 26, 2011, 01:21:04 pm »
Like graphmastur said, you need to tell the compiler where the wx headers are. That's actually pretty easy since it looks like you're using a Linux system. To do this, run the following commands:
g++ -c `wx-config --cxxflags` helloWorldGUI.cpp
g++ -o helloWorldGUI helloWorldGUI.o `wx-config --libs`
The first command compiles your source file helloWorldGUI.cpp and creates the object file helloWorldGUI.o. The "wx-config --cxxflags" command tells g++ where the wx headers are.
The second command links the object file helloWorldGUI.o into an executable file named helloWorldGUI. The "wx-config --libs" command tells g++ where the wx libraries are.
Both of the wx-config commands above print out the appropriate flags for the compiler/linker (g++), and they are put inside backticks `` so their output is inserted directly into the g++ command lines.
EDIT: jimbauwens makes a good point in the post after mine. Make sure you have the dev or devel version installed, and then you can run the commands above.
44
« on: March 25, 2011, 08:31:51 pm »
How does the calculator even detect that code is running in the "illegal" area? The only explanation that I can think of is that the last two bits on the address bus (the ones that must be on if code above C000 is being executed) are wired into a trigger that causes the processor to jump to the boot code. In other words, the detection is in the hardware itself.
Most likely it is. Remember that we are talking about all of this being in the processor. So the processor knows immediately if the pc is C000h or above.
Which probably explains why the Z80 processor is actually TI's modified version.
The detection may actually be done outside of the Z80. The memory controller could detect multiple consecutive accesses (which indicates instruction fetches) to a particular memory range and do almost anything it wants at that point.
45
« on: March 25, 2011, 08:00:45 pm »
FWIW, the only non-hexadecimal characters in that huge blob of characters are in the first several characters (".TESTAPP" and "Asm("). The rest are only 0-9A-F.
EDIT: Also, if a disassembler takes 10-15 minutes to disassemble a small program like that, there is something wrong with that disassembler! I wrote a simple disassembler that disassembled the 128K ROM of the TI-86 in about a second.
|





