Ah ok thanks for the info. I guess someone could write an emulator later maybe, but if there are games that don't use a single AMS command or whatever they are called on 68K calculators I bet they wouldn't be too hard to port.Also I assume of of your goal for this OS will be a much smaller file size than TI-AMS to give as much free RAM/archive as possible to the user? I wonder how much flash memory does a TI-89 and a TI-89T has in total...

Wel, it also depends on whether the game does stuff like installs its own interrupt handler. I believe TI-AMS allows user programs to run code in supervisor mode without too many restrictions (there are some restrictions on writing to Flash, though), but Punix keeps a clear separation of kernel (supervisor) mode and user mode. Also if it tries to read and write directly to the keyboard I/O ports (these are actually mapped to memory addresses in 68k), it would interfere with the normal keyboard handling code. So... it all depends on how much a program tries to do that is allowed by TI-AMS but not by Punix. In a way, it would be similar to porting a game or application from MS-DOS to Windows or Unix/Linux, since MS-DOS allows direct hardware access and the others don't.

Yes, one of my goals is to leave as much RAM and FlashROM space to the user as possible. The FlashROM is the filesystem, which leaves all of RAM for kernel buffers and user programs. Incidentally I recently tested how much contiguous memory I could allocate from userspace using malloc(). I started trying to allocate 256K (this is how much RAM the TI-89/92+ have total), reduced the amount by 1024 bytes until the malloc() succeeded, and then printed that amount (and free()ing the memory, of course!). In my current test setup, that amount came out to 202752 bytes, or 198 Kbytes. In the past I cleared out some large static memory allocations in the kernel, but there is still some kernel memory that I can free up for user programs here and there.

The TI-89 and TI-92+ have 2MB of FlashROM, I think the TI-89T has 4MB. Currently the Punix kernel uses two pages of FlashROM, or 128K, which leaves 1.875 MB for the filesystem (which I'm still writing). Some of the filesystem will be used for system binaries and configuration files, so the user should have maybe 1.5 MB for their files. Compare this to 700K (or 2.7MB on the TI-89T) of FlashROM available to the user in TI-AMS. All that math software takes up a lot of space (and poorly optimized code doesn't help either.)

As for the site, I guess you probably signed up on the other Omnimaga board back in 2006-07 but never posted. I remember at one point we had registrations disabled, though, because of spambots, then later we added a different registration step to block them, while still allowing people to sign up, but some people would never complete it. I think I might have seen you in #tcpa or something, too.

That sounds about right. I think that is what happened.

Ok, so I know most people here use Z80, but here is a set of 68k routines for shifting unsigned 64-bit numbers left and right. I wrote these for a floating-point emulator that I'm writing, but they're useful for other stuff too.

.equ SHIFT_THRESH, 5 | XXX the exact optimal value needs to be figured out

| unsigned long long sr64(unsigned long long, unsigned);
sr64:
        move.l  (4,%sp),%d0
        move.l  (8,%sp),%d1
        move.w  (12,%sp),%d2

| shift right a 64-bit number
| input:
|  %d0:%d1 = 64-bit number (%d0 is upper 32 bits)
|  %d2.w = shift amount (unsigned)
| output:
|  %d0:%d1, shifted
sr64_reg:
        cmp     #SHIFT_THRESH,%d2
        blo     8f
        cmp     #32,%d2
        bhs     5f
        ror.l   %d2,%d0
        lsr.l   %d2,%d1         | 00..xx (upper bits cleared)

        move.l  %d3,-(%sp)

        | compute masks
        moveq   #-1,%d3
        lsr.l   %d2,%d3         | 00..11 (lower bits)
        move.l  %d3,%d2
        not.l   %d2             | 11..00 (upper bits)

        and.l   %d0,%d2         | only upper bits from %d0
        or.l    %d2,%d1         | put upper bits from %d0 into %d1
        and.l   %d3,%d0         | clear upper bits in %d0

        move.l  (%sp)+,%d3
        rts

        | shift amount is >= 32
5:
        cmp     #64,%d2
        bhs     6f
        sub     #32,%d2
        move.l  %d0,%d1
        lsr.l   %d2,%d1
        moveq   #0,%d0
        rts

        | shift amount < threshold
7:
        | shift right one bit
        lsr.l   #1,%d0
        roxr.l  #1,%d1
8:
        dbra    %d2,7b
        rts

| unsigned long long sl64(unsigned long long, unsigned);
sl64:
        move.l  (4,%sp),%d0
        move.l  (8,%sp),%d1
        move.w  (12,%sp),%d2

| shift left a 64-bit number
| input:
|  %d0:%d1 = 64-bit number (%d0 is upper 32 bits)
|  %d2.w = shift amount (unsigned)
| output:
|  %d0:%d1, shifted
sl64_reg:
        cmp     #SHIFT_THRESH,%d2
        blo     8f
        cmp     #32,%d2
        bhs     5f
        rol.l   %d2,%d1
        lsl.l   %d2,%d0         | xx..00 (lower bits cleared)

        move.l  %d3,-(%sp)

        | compute masks
        moveq   #-1,%d3         | mask
        lsl.l   %d2,%d3         | 11..00 (upper bits)
        move.l  %d3,%d2
        not.l   %d2             | 00..11 (lower bits)

        and.l   %d1,%d2         | only lower bits from %d1
        or.l    %d2,%d0         | put lower bits from %d1 into %d0
        and.l   %d3,%d1         | clear lower bits in %d1

        move.l  (%sp)+,%d3
        rts

        | shift amount is >= 32
5:
        cmp     #64,%d2
        bhs     6f
        sub     #32,%d2
        move.l  %d1,%d0
        lsl.l   %d2,%d0
        moveq   #0,%d1
        rts

        | shift amount is >= 64
6:
        moveq.l #0,%d0
        move.l  %d0,%d1
        rts

        | shift amount < threshold
7:
        | shift left one bit
        lsl.l   #1,%d1
        roxl.l  #1,%d0
8:
        dbra    %d2,7b
        rts

These routines can be used from assembly (using the _reg versions) or from C (using the non-_reg versions).

Also, if most shifts in your program are more than the threshold (SHIFT_THRESH), you can remove the 2 instructions at the beginning and 4 lines at the bottom of both routines (in the _reg versions, that is). That would save a bit of time (for most cases) and some space.

Without the threshold sections, these routines seem to be smaller (and probably faster) than the assembly code generated by TIGCC for shifting 64-bit numbers ("long long" type). My code does check for shifts greater than 64, whereas TIGCC doesn't (shifts greater than the width of the type produce undefined results in C anyway, but I wanted defined behavior in my code).

I'll double-check the sizes and timings in mine relative to the generated code and then bring this to the TIGCC maintainers' attention if mine is better. Smaller and faster code is always a good thing, right?

Recently I started experimenting with floating-point emulation on the 68K calculators, specifically in my own OS, Punix. (I'm new to this forum, and I haven't talked about Punix lately in other TI forums either, so for those who don't know what Punix is, it's a Unix-like OS--complete with features like preemptive multitasking and a VT220 terminal emulator--that I'm writing for the TI-92+ and maybe the TI-89)

Here's a little background on floating-point emulation. First of all, the 68000 processor has no support for FP hardware (such as the 68881 floating-point unit, or FPU). Only the later CPU's in the family (68020, '40, '60) do. However, the 68000 does have an exception vector (the so-called "F-line" or "Line 1111 emulator" exception) which allows for software FP operations. This is basically an FPU emulator, and this is what I have done. Needless to say, the software FP emulation is far slower than a real FPU by about an order of magnitude in the best case.

The 68881 and 68882 are the FPU's of choice for the 68020 (and also for the FPU-less versions of the '40), so this is what I chose to emulate. This FPU supports several integer and floating-point formats (byte integer, word integer, long integer, single-precision float, double-precision float, extended-precision float, and packed decimal float) and several addressing modes (AFAICT, the same modes as the 68000). The internal FP registers of the 6888x FPU's are 80-bit extended-precision (but stored in 96 bits), as described on this page: http://en.wikipedia.org/wiki/Extended_precision

By contrast, the TI-AMS on the 68k calcs uses an 80-bit SMAP II BCD floating-point format, which has less precision, a smaller range, and is slower to calculate than extended precision. (Single precision is smaller and faster than the others, but it also has the least precision and smallest range.)


Anyway, after a few hours of work, I implemented basic instruction decoding and the execution of a few simple FP instructions, notably FTST, FNEG, and FBcc (which is analogous to the regular Bcc instructions). Here is some demo code showing what my FPU emulator can handle so far:

| print the FP type using the current FP condition codes
printfptype:
movem.l %a0-%a3,-(%sp)

| test for nan
fbngle  1f | NGLE = not greater, less, or equal

| test for zero/not zero
fbneq   2f | NEQ = not equal
pea.l   4f      | 0
bra     3f
2: pea.l   5f      | x
0: bra     3f

1: pea.l   9f      | nan

| test for sign (doesn't recognize negative zero)
3: fblt    2f      | LT = less than
pea.l   7f      | +
bra     0f
2: pea.l   6f      | -
0: pea.l   8f

jbsr    printf
lea.l   (3*4,%sp),%sp

movem.l (%sp)+,%a0-%a3
rts

4: .asciz "0"
5: .asciz "x"
6: .asciz "-"
7: .asciz "+"
8: .asciz "%s%s\n"
9: .asciz "nan"

| here is the main entry point for the demo
| fputest() is called from a user-space driver program
.global fputest
fputest:
move    #-5,%d0

| %Dn.b
fneg.b  %d0,%fp0
bsr     printfptype

| (d16,%pc)
fneg.x  (11f,%pc),%fp1
bsr     printfptype

| (An)
lea     11f,%a3
fneg.x  (%a3),%fp2
bsr     printfptype

| (An)+
fneg.x  (%a3)+,%fp3
bsr     printfptype
fneg.x  (%a3)+,%fp4
bsr     printfptype
fneg.x  (%a3)+,%fp5
bsr     printfptype
fneg.l  (%a3)+,%fp6
bsr     printfptype
fneg.l  (%a3)+,%fp7
bsr     printfptype
fneg.w  (%a3)+,%fp0
bsr     printfptype
fneg.w  (%a3)+,%fp1
bsr     printfptype
fneg.b  (%a3)+,%fp2
bsr     printfptype
fneg.b  (%a3)+,%fp3
bsr     printfptype

| -(An)
fneg.b  -(%a3),%fp4
bsr     printfptype
fneg.b  -(%a3),%fp5
bsr     printfptype
fneg.w  -(%a3),%fp6
bsr     printfptype
fneg.w  -(%a3),%fp7
bsr     printfptype
fneg.l  -(%a3),%fp0
bsr     printfptype
fneg.l  -(%a3),%fp1
bsr     printfptype

rts
11: .long 0x7fffffff,0x40000000,0x00000000  | nan
12: .long 0x7fffffff,0x00000000,0x00000000  | +inf
.long 0xffffffff,0x00000000,0x00000000  | -inf
13: .long 7
.long -7
.word 5
.word 0
.byte 3
.byte 0

This code tests a few different addressing modes (register, indirect, address register indirect, address register indirect with pre-decrement/post-increment) and integer/float formats (extended-precision, long, word, byte). My emulator cannot handle single- or double-precision or packed decimal formats yet, so I haven't tested those.

The output of this code is "-x" for a negative number, "+x" for a positive number, "+0" for zero (the test code doesn't differentiate between positive and negative zero), or "+nan" for NaN.

Here is a screenshot of this demo code in action:



(You may notice that it displays "+x" for both infinities, whereas it should display "-x" for negative infinity. I already fixed this bug but didn't update the screenshot.)

Each emulated instruction takes between about 600 and 1400 cycles, which is between 8.5 and 20 KFLOPS (kilo floating-point operations per second) with a 12MHz clock rate. According to http://en.wikipedia.org/wiki/Motorola_68881 the 68881 runs at 160 KFLOPS at 16MHz, which would be about 120 KFLOPS at 12MHz. As you can see, this FPU emulator is about 1/10 as fast as a real FPU. (Take these with a grain of salt as I haven't really started on the more computationally expensive operations like multiplication and division).

Since this demo only tests simple operations (fneg is basically just flipping a single bit), most of the time in these simple FP operations is spent in decoding the instruction itself. I might also make the bare floating-point routines available to user programs (so they can do, eg, "bsr fneg" to negate (%a0) and put the result in (%a1)) to remove the instruction decoding time, but for now I'll stick with this FPU emulation.

Edit: fixed note about the bug regarding +/- infinity. I was off by one looking at the display.
Edit again: negative infinity bug is squished! I didn't check the sign for infinity and nan in the FTST code (which FNEG does implicitly)
Edit thrice: I just realized that an extended-precision value with a maximum exponent (0x7fff) is a NAN only if the fraction (excluding the MSB of the fraction) is non-zero. If only the MSB of the fraction is set, it's an infinity, not a NAN. I fixed my code to reflect this correction. Read this for (many) more details: http://www.freescale.com/files/archives/doc/ref_manual/M68000PRM.pdf

QuoteBegin-Netham45+20 Jan, 2007, 21:45-->

QUOTE (Netham45 @ 20 Jan, 2007, 21:45)

dude.... those are awesome.

c1-->

CODE

ec1fish0: ; tail out   86 Art / Go Fish « on: January 17, 2007, 08:12:00 pm » Here's a quick-and-dirty animation I made of a fishy: 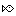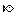Here's each frame (all 2 of them!) separated but in the same image: Is that along the lines of what you want? 87 TI Z80 / Not another ti shell « on: December 28, 2006, 08:59:00 am » QuoteBegin-CureDesu+27 Dec, 2006, 23:39--> QUOTE (CureDesu @ 27 Dec, 2006, 23:39) That would be pretty damn awesome if it was possible to run C on Z80 calcs. Pages: 1 ... 4 5 [6] SMF 2.0.15 | SMF © 2017, Simple Machines Dream Portal 1.1 © 2009–2024 Dream Portal Team XHTML RSS WAP2 Server load over the past 5, 10 and 15 minutes respectively: 0.55517578125, 0.3916015625, 0.31982421875 Page created in 0.108 seconds with 28 queries.