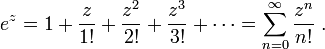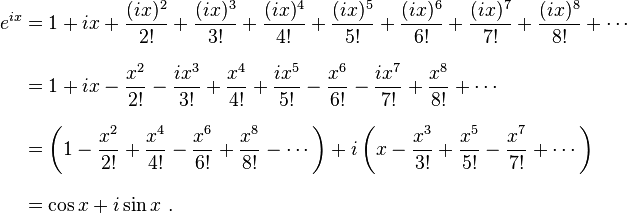e^(pi i) does not equal e^(pi)*e^(i)

@ruler501, check this link: http://en.wikipedia.org/wiki/Euler's_formula#Proofs It's a bit hard to understand without a backing in calculus though

Generally you can't really conceptualize raising a number to an imaginary power; the main method of going about this sort of thing is creating a power series (a polynomial) that mimicks the behavior of e^x. e^x's power series (which, when taken to an infinite amount of terms is perfectly accurate) then can be used with imaginary values for x and still make sense.
e^x's power series looks like this:

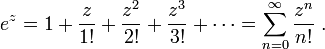
and so e^(ix)'s power series looks like this:

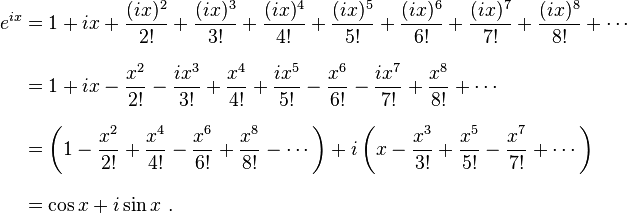
You'll have to take my word for it that that series is actually cosx+i*sinx. The rest of the proof goes from there.

Even better, Axe code:
{_E8447}->VAR

Also nice to hear this is back up.

The lowercase letters are 2 byte tokens:

BB66 = f
66 = Normal

Check out the xml's included with Merth's Tokens (maybe you can get them other places, idk)

I really like the look of these calcs too, I thought the prizm looked too much like a cell phone The old Nspire is just hideous as well.

So according to our trusty calculators...

              __
(1/2)!=(1/2)\/pi
              __
(3/2)!=(3/4)\/pi
               __
(5/2)!=(15/8)\/pi
                 __
(7/2)!=(105/16)\/pi
                 __
(9/2)!=(945/32)\/pi
Now, my question is...Why?

Huh. Well, you learn something new every day!

Wow, this opt is incredible O.o

Been slowly chipping away at the mountain of data to be entered. Finished up a few tilesets, and I've been working on the story a bit as well. The next village is almost done, just have to add the NPC convos.

Also, optimized 150 more bytes off the main app, and the amount of free RAM required is about to take a dip as well